Benefit of Rounding Cents
Faster calculations
Skip the pennies - it’s easier to count with round numbers. Rounding cents on payments makes transactions easier to calculate and receipts more readable for both employees and customers.
Round invoices
Enable the Round invoices under the POS settings -> Configuration -> Payment section to round the total price of the shopping cart if price is decimal. The rounding performs already in the shopping cart: product prices leave with the original price (not rounded), but the total field will show rounded amount.

Adding Cent Rounding only for cash payments
In the POS, navigate to the Settings -> Configuration -> Payment -> Round cash payments to nearest x cents.
Check off the box and insert the amount you wish to be rounded up. Then select needed rounding algorithm from the “using algorithm” dropdown list. Save changes.

Cash Payament Rounding algorithms
Symmetric algorithms
(if X rounds to Y, -X should always round to -Y)
- Round away-from-zero - this refers to rounding in such a way that the result heads away from zero. For example, 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, and 3.9 will all be rounded to 4. Similarly, -3.1, -3.2, -3.3, -3.4, -3.5, -3.6, -3.7, -3.8, and -3.9 will all be rounded to -4.
- Round toward-zero - as its name suggests, this refers to rounding in such a way that the result heads toward zero. For example, 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, and 3.9 will all be rounded to 3. Similarly, -3.1, -3.2, -3.3, -3.4, -3.5, -3.6, -3.7, -3.8, and -3.9 will all be rounded to -3.
- Round towards-even - values are rounded toward the nearest even number Thus, 3.1-3.9 and 4.1-4.9 will be rounded toward 4, 5.1-5.9 and 6.1-6.9 will be rounded toward 6.
- Round towards-odd - values are rounded toward the nearest odd number. In this case, 2.1-2.9 and 3.1-3.9 will round to 3, 4.1-4.9 and 5.1-5.9 will round to 5.
Examples of symmetric algorithms that are rounded to an integer:
Name
Example | away-from-zero | towards-zero | towards-even | towards-odd |
| 0.4 | 1 | 0 | 0 | 1 |
| 1.6 | 2 | 1 | 2 | 1 |
| 2.6 | 3 | 2 | 2 | 3 |
| 3.4 | 4 | 3 | 4 | 3 |
Examples of symmetric algorithms that are rounded to the nearest integer:
- Half-away-from-zero - half values are rounded way from zero. In this case, 3.1-3.4 will round to 3, 3.5-3.9 will round to 4.
- Half-toward-zero - half values are rounded toward zero. Thus, 3.1-3.5 will round to 3, 3.6-3.9 will round to 4.
- Half-towards-even(banker's rounding) - only half values are rounded toward the nearest even number (3.5 will round up to 4 and 4.5 will round down to 4). Other values are rounded to the nearest integer by default. This algorithm is, by definition, symmetric for positive and negative values, so both -3.5 and -4.5 will round to -4.
- Half-towards-odd(banker's rounding) - only half values are rounded toward the nearest odd number (3.5 will round down to 3 and 4.5 will round up to 5). Similarly, -3.5 will round to -3, and -4.5 will round to -5. Other values are rounded to the nearest integer by default.
Name
Example | half-away-from-zero | half-towards-zero | half-towards-even | half-towards-odd |
| 0.5 | 1 | 0 | 0 | 1 |
| 1.5 | 2 | 1 | 2 | 1 |
| 2.5 | 3 | 2 | 2 | 3 |
| 3.5 | 4 | 3 | 4 | 3 |
Asymmetric algorithms
- Up - this round-up acts in the same manner as the away-from-zero algorithm, but negative values in this case will be rounded asymmetrically. For example, 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, and 3.9 will all be rounded to 4. But, -3.1, -3.2, -3.3, -3.4, -3.5, -3.6, -3.7, -3.8, and -3.9 will all be rounded to -3.
- Down - this round-up acts in the same manner as the towards-zero algorithm, but negative values in this case will be rounded asymmetrically. For example, 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, and 3.9 will all be rounded to 3. But, -3.1, -3.2, -3.3, -3.4, -3.5, -3.6, -3.7, -3.8, and -3.9 will all be rounded to -4.
- Half-up - in case of the positive values first five of them 3.0 through 3.4 to round down to 3, and for the remaining five values 3.5 through 3.9 to round up to 4. In the case of the negative values -3.1, -3.2, -3.3, -3.4,and -3,5 these will all round to the nearest integer, which is -3; similarly, in the case of values like -3.6, -3.7, -3.8, and -3.9, these will all round to -4.
- Half-down - in this case, a half-way positive value such as 3.5 will round down to 3. In the case of an asymmetric implementation of the algorithm a value of -3.5 will actually round to -4.
Examples of asymmetric rounding algorithms:
Name
Example | up | half-up | down | half-down |
| 0.4 | 1 | 0 | 0 | 0 |
| -0.4 | 0 | 0 | -1 | 0 |
| 0.5 | 1 | 1 | 0 | 0 |
| -0.5 | 0 | 0 | -1 | -1 |
| 0.6 | 1 | 1 | 0 | 1 |
| -0.6 | 0 | -1 | -1 | -1 |
NB! In case of “0” value it means that POS will leave the initial value as is.
Example:
The 0.4 is rounded by the half-up algorithm. According to the result in the table it should be “0”, but the product which has a price 0<, can not be sold for free. Therefore the POS will not round this amount and leaves it with the initial value.
Note: current setting relates only to cash tender payments.
Also the Brazil POS has an option to show a "Change" field in the Payment Modal component that shows to the user what the expected change value would be after the document rounding has been applied. The option is called Show expected "Change" sum in Payment Component. The setting can be enabled in the POS settings -> Configuration -> Payment.
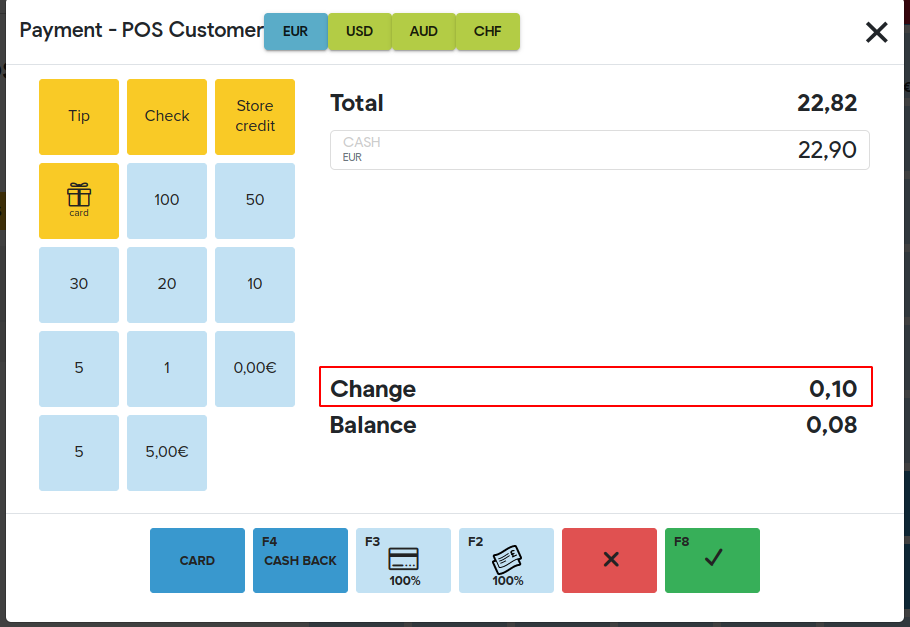
Rounding “Change”
If calculating the change/balance, the POS will invert the algorithm:
- While using Up or Down algorithms then algorithms will swap places based on the used one(total is rounded by Up, then “change” amount will be rounded by Down and vice versa).
- If Odd is used then “change” amount will be rounded by Even.
- If Even is used then nothing changes and "change" will be rounded by Even.
- Other algorithms remain unchanged.